$C_0$-semigroups
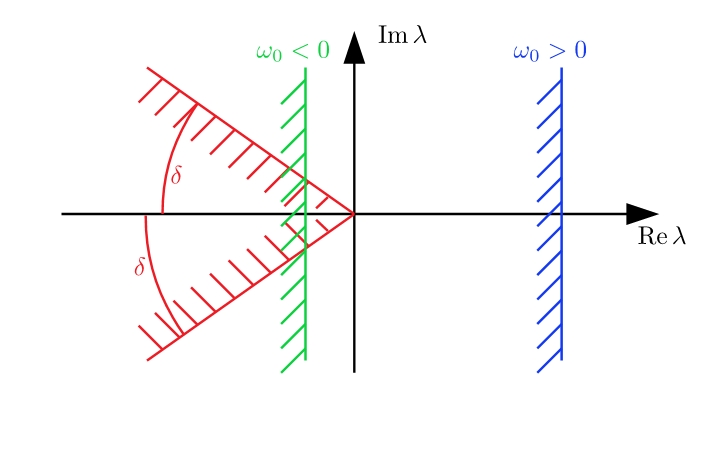A $C_0$-semigroup is characterized by its growth bound $\omega_0$ and the spectrum of its generator lays to the left from the line ${\rm Re},z=\omega_0$ in the complex plane. A necessary condition for the uniform exponential stability of a $C_0$-semigroup is $\omega_0<0$. A generator of an analytic semigroup has its spectrum within a sector of angle $0<\delta<\frac{\pi}{2}$ from the negative real diection.
In the setting of partially ordered banach spaces me and Prof. Mikhail Igorevich Kamenskii have proven necessary and sufficient conditions for a $C_0$-semigroup of the form $e^{(-\Gamma+M)t}$ to be stable. The generator $-\Gamma+M$ is a (possibly) unbounded linear operator $-\Gamma$ perturbed by a bounded, positive (in the sense of the partial order structure) linear operator $M$. Our main requrements are that the unperturbed semigroup $e^{-\Gamma t}$ is stable and the product $\Gamma^{-1}M$ is contracting.
Ivan Gudoshnikov
My current research is on Moreau’s Sweeping process, its stability and appications.